太喜欢了！数学

　　生命游戏是产生并自我组织的一个例子。计算机科学、物理学◆■◆、生物学、生物化学、经济学、数学、哲学和生成科学等各个领域的学者都可以用这种通过执行简单规则即可产生复杂模式的方式去进行更多的研究★★★★◆■。未来会被运用到什么领域，犹未可知。

　　★◆◆◆◆★“载入史册”发布会后■◆★◆★，特斯拉跌超8%，市值蒸发4395亿元◆■◆★■◆！发生了什么■◆■★■■？

　　毕节13岁女孩深夜翻阳台后被白车接走离家8天■★，父亲：回来了，正在派出所

　　这两年■★◆★■，在成都像Domath一样做趣味数学的工作室多了起来★◆，他们带孩子们玩起了更有意思的数学。姚工觉得这是很好的，但是也担心会造成新的问题★◆◆■，有时候越想抓住一个东西★◆◆■★，往往越抓不住。

　　接触了数学教育之后，他就很想弄清楚我们为什么要学数学★■◆★■，■◆★■◆“掉进数学的坑里研究了很久之后◆◆■★，我发现数学本质上是一种世界性的语言■■■■，我们不用见面★★★，不用说话◆■★■◆，我们可以用数学公式进行交流。◆◆★■■★”

　　一般人的放松方式，可能是运动、购物、阅读、刷短视频等，很少有人会用数学的方式进行自我放松■★★◆■◆。姚工有以解数学题来放松的朋友■★◆◆★★，他自己则喜欢做数学作品■◆★◆■■。

　　Y★■：好的问题，首先是有趣的，其次是经典的。这种经典最好能跟数学史联系，孩子可以通过解答这个题目，和几百年、几千年前的人建立一种连结★★。最后，我希望问题有纵深★◆■■■◆，一个问题可以成为一个桥梁，可以延展到其他问题上去。

　　上交所：10月8日至10月11日对144起证券异常交易行为采取了书面警示等监管措施

　　Y：《迷人的数学》《数学简史》《数学的力量》《太喜欢了★■◆◆！数学》《给孩子的数学实验室》。

　　姚工拿出一个喝水的纸杯，问我让它自然滚动起来◆★◆■★◆，会不会回到手上◆◆★■★★。我滚动了好几次，纸杯都回到了我手里。

　　几行代码展示出来的真的是生命的本质吗■◆■■★？我没有答案■★◆◆★■，但换一种方式看待生命，是不是挺好■◆？

　　这里不像是教室，更像是游乐场，看似不起眼的一张图表、一个球体◆■◆，都暗含着数学里的某个原理、公式。孩子们在这里一起解题★■★■，一起探索■◆★，一起动手，感受数学之美。

　　Domath的工作室是两居室，客厅里的书架上摆放着几千册与数学有关的书籍，还有许多老师和孩子们一起做的数学作品★■★◆。墙上贴着不少图形，每一幅都与数学有关。角落里的3D打印机正在滋滋滋打印着约翰逊多面体（1966年，美国数学家诺曼·约翰逊发现了92种约翰逊多面体。1969年，维克托·查加勒证明约翰逊多面体只有92个。）

　　除了永恒性，数学还具有抽象性，“这就是数学为什么难学的原因◆■◆■。数学本质上是一个抽象的学科★■◆◆■★。你看，这是5个手指，这是5支铅笔，但这个世界上到底有没有5本身■◆？”

　　Y：家长首先要做的是更新自己的数学认知、数学教育观念◆◆，尽量给孩子带来更好的数学体验■◆，打开数学思维。其次要弄清楚学数学的目的◆★，如果家长是摇摆的，举棋不定的，那他很难有独立的思考和认知◆◆★★，很容易受环境的影响，这就意味着孩子不太能获得与之匹配的支持。

　　事实上★★■■◆，姚工并不是从小就热爱数学的天才，他在几年前才开始被数学所吸引，“我从小生活在江苏的乡村，成绩并不拔尖■■◆■，语文很不好，靠数学成绩拉平均分，那时候也没有体会到太多学习数学的乐趣。高中时很喜欢文言文★★★■，觉得太精妙了★◆★，一个那么简洁的词，却能表达丰富的意思◆◆■，这一点很吸引我，而且节奏感也很好◆◆◆，现在数学吸引我的也是这些。”

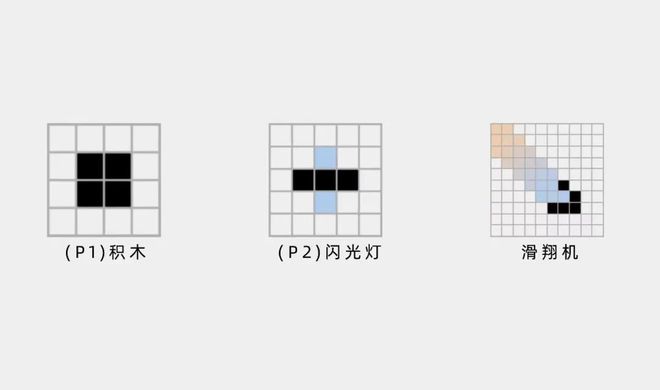
　　最后★◆★■◆◆，我问姚工最喜欢的数学家是谁◆◆■，他说是英国数学家约翰·何顿·康威，他给我讲起了康威生命游戏（Conways Game of Life）■★■◆◆■，又称康威生命棋的玩法。

　　“一次性纸杯滚两头粗细不一样★★■★，如果我把它延伸出去，其实是一个圆锥，它滚动的轨迹是一个圆环。你看我只要把一个圆柱收一下，它就变成了一个圆锥◆■★◆■。这是不是意味着★■◆◆■，我们在学习圆柱和圆锥的体积公式时，可以把它们统一起来。”

　　不同的开局状态，最后就会呈现不同的结果■◆■★■。坐在电脑前，姚工给我演示了10多种游戏运行的方式◆◆，他演示得很认真，并在过程中陷入思考★★■◆。

　　另一边靠墙的柜子上摆着不少阿基米德多面体■■，“它们是以两种及以上正多边形为面的凸多面体，并且都可以从正多面体经过截角、截半、扭棱等操作构造。阿基米德体共有13种■★◆，其每条边的长度相同，每个顶点也都全等。”

　　尽管这个游戏中的规则是完全确定的，但是很难预测几个步骤后的状态■★★■■◆。简单来说，该游戏是零玩家游戏，这意味着我们只能设定其初始状态，并观察其演变，它的发展由其初始状态决定。

　　千万粉丝博主账号被封■◆★◆◆！曾建议网友8号全仓炒股，旗下单个业务收入可达7000万

　　约翰逊多面体★■★◆■、阿基米德多面体◆■★★、柏拉图多面体……等等，作为数学盲，我的脑子不够用了■■◆。

　　这时我发现房间的一角放着一个由许多冰淇淋纸筒组成的球体■◆★★■◆，“像不像你去买西瓜时，老板取出一小块给你品尝的样子◆◆★★■◆。”嗯■★◆，像★★◆★。

　　·一个网格所代表的细胞周围有8个相邻的网格，通常用黑和白两种颜色来分别代表网格上的细胞的生和死。（图源

　　我突然理解了《数学的力量》一书中作者所写◆◆★:数学能把你的大脑变成一个游乐场。适时适量地研习数学，其实就像游戏一样：探索规律时的灵光一现会让你欢呼雀跃★★，发现事物的运转方式也会让你陶醉不已。

　　首先，数学是他的热爱，他尽量每天都刨出时间学一点数学知识，思考一些数学问题■◆，放松的时候呢，就做几件数学作品。要是条件允许，他想重新回到学校★◆，学习拓扑学（拓扑学是由几何学与集合论里发展出来的学科，研究空间、维度与变换等概念）。

　　大学学习土木工程★◆■■■，毕业后在杭州做过几年桥梁工程师的姚工■◆■■◆◆，为什么来到成都做起了创新教育，并不是个复杂的故事，一切只是听从内心的指引◆■◆。

　　我们习惯于盯着某个领域最了不起的人，反倒忽视了■★★，一个普通人应该怎样和数学相处■◆★■。了不起的数学家可以改变世界，但是这个世界不只有那些最顶尖的数学家，还有很多普通的数学家■◆◆，还有很多普通人■◆。难道数学的大门就对他们早早关上了吗★■■？

　　“其实我们做的是一份开窗的工作★◆★■★，我们学习了很多数学相关的东西，经过筛选，把认为好的数学问题带给孩子们和家长。了不起的是他们，他们知道什么叫享受数学◆◆。”

　　Y：先弄清楚想学习的是数学的哪一个类别，我个人觉得最好的方式是找经典的教材来慢慢啃。一开始可能会比较枯燥★■◆■◆◆，当你理解了之后，会发现很多乐趣■◆■■◆■，这种正向反馈会激发你更深入地去学习。数学是一个逻辑性很强的环环相扣的学科，很难跳跃式学习■■★◆◆，必须一步步建立逻辑性的阶梯，你才更能够更好地理解它的魅力。

　　不愧为数学家之乡■◆！第40届全国高中数学竞赛获奖名单公布◆★◆：温州17人入选省队◆★■■■！41人获得省一！

　　搜索引擎的核心算法是线性代数★◆；各种广告之所以会被推送到我们面前是基于博弈论……数学与我们的日常生活有着千丝万缕的联系。但如果一个人不想去搞计算机，而是想成为插画师，还要不要学数学呢★◆？

　　“数学有永恒性★■◆★，一旦被证明的东西，就不会再在逻辑上被证明了，但是它会发展，会丰富。比如说三角形的内角和都是180度■◆◆◆，这个问题仅限于在平面几何中，后来有数学家提出，在球面上■★★，或在一个马鞍的曲面上的三角形，内角和就不是180度了★◆■★■。■◆◆◆■”

　　“我比较在意数学作品的艺术性★■，因为我一直认为好看很重要◆◆■★■，但是数学的好看和其他的好看不一样，当你用数学的眼光去欣赏一些东西★■■★★，会带来一种高级感◆■★◆◆。比如看油画，我习惯用数学逻辑性去欣赏，去看它的对称性和空间感，因此我更喜欢古典的作品。比如这个著名的黄色边框是美国《国家地理》杂志的品牌标志，长方形长和宽是黄金比例，挺有意思。成都街头桂花飘香的时候■◆★★★■，不知道你有没有注意，桂花花瓣的对称轴不是1条■◆■★★，可能是3条或者4条……★■★■”

　　特别声明：以上内容(如有图片或视频亦包括在内)为自媒体平台“网易号◆★■”用户上传并发布★■■★■，本平台仅提供信息存储服务★◆■◆◆★。

　　葱花由很多个五角星组成花球；苹果切出五角星；长在地里的叶子菜，需要按比例交错生长，才能长出更多的叶子……

　　姚工的答案是：不学数学，可能不会影响我们的生存，但数学给我们提供的是理解世界万事万物的一种思维方式，它让生命有更丰富的体验■◆★◆■★。

　　其次◆■★★◆★，数学是他的事业，2020年■■◆◆★，他和伙伴一起在成都创立了Domath思维实验室，他们的slogan是：为数学辩白，为工程播种。

　　数学是巨浪，在巨浪中的小舟上◆◆◆■■，姚工每天都在一边完善小舟，一边往前划船，也期待更多小舟出现■◆■★◆。

　　一棵树为什么那样生长★★■◆★◆？背后的数学语言是什么？“我们曾经做过一个项目■◆■★◆，叫美丽的平行线，带孩子们用数学的方式去观察树，最后发现每一棵树都隐藏着无数组的平行线。”

　　生活中，我们遇到的大部分知识都会涉及视角、不确定性、信息不全等问题，但数学真理不一样◆★，它一直在那儿■◆，让我们信任理性。

　　姚工觉得不是这样的，数学可以丰富一个人的生命■★■★，“体会到数学的快乐需要具备一定的能力，在这之前，你要先学会臣服在它的下面，你得遵循它的规则★■★★★，利用它的规则去解决问题，然后再继续学习新的规则■■★★。当你掌握了数学密码，你就具有了创造力。◆★◆■★■”

　　从数学这一角度看待事物★◆★★★，姚工说自己对这个世界更敬畏了◆★，觉得自己更渺小了。

　　无论用5乘以哪个数字★◆★★◆◆，都不会改变这个数字的奇偶性；无论怎么旋转一个三维几何体，都不会改变它的体积◆★◆◆◆★。这些★★◆◆■◆，是数学里的不变量■◆◆★■，也称之为数学的永恒性。

　　这也是为什么姚工喜欢带着孩子们做数学实验、数学作品，玩数学游戏的原因。实物用多了，自然脑子里那种形象化、抽象能力就提高了■■。“如果一个人抽象能力很好，数学不太可能学不好◆■★★★。”

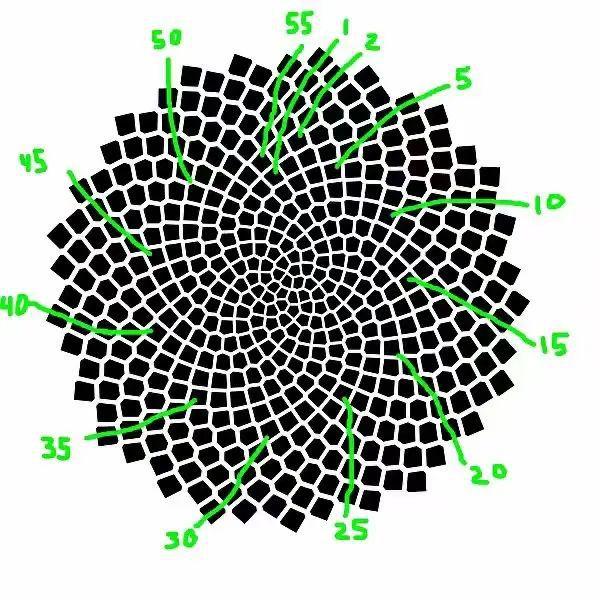
　　见到满山的向日葵，他满眼的黄金比例角（137.51度）◆★■★◆，满脑子的最无理的无理数（黄金分割比）★◆★，他认认真真地数了数向日葵的螺旋线。

　　在我看来■■◆，诗人只有去感知别人未曾感知的东西，才能比别人看得更加深刻■◆★◆★。数学及亦如此。——索菲娅·柯瓦列夫斯卡娅

　　太难了！网传杭州大厂裁员，10月走N+2，11月走N+1，涉及上千人…

　　每经历一次纯粹的思考，都会有一些永恒的、实质的东西嵌入我们的灵魂。——伯恩哈德·黎曼

　　今年儿童节，Domath在2000平的空间里◆■★■，做了一场名为3n+1的数学文化节◆★★◆■，用游戏、图像、数学装置来重新打开我们对数学的理解。两天里，有600多个人通过买票参与其中。“虽然门票挺贵的，但是场地租用费，加上现场展品的制作，成本挺高的，最后其实还是亏了一些钱■■◆■，但我觉得很有价值◆■◆。”